Шифрование с открытым ключом
Шифрование с открытым ключом является более поздней технологией, чем шифрование с секретным ключом. Главным различием между этими двумя технологиями является число ключей, используемых при шифровании данных. В шифровании с секретным ключом для шифрования и дешифрования данных используется один и тот же ключ, в то время как в алгоритмах шифрования с открытым ключом используются два ключа. Один ключ используется при шифровании информации, другой - при дешифровке.
В чем заключается шифрование с открытым ключом?
На рисунке 12.8 показана базовая схема шифрования с открытым ключом (асимметричного шифрования). Как видно из рисунка, оба абонента (и отправитель, и получатель) должны иметь ключ. Ключи связаны друг с другом (поэтому они называются парой ключей), но они различны. Связь между ключами заключается в том, что информация, зашифрованная с использованием ключа K1, может быть дешифрована только с помощью его пары - ключа K2. Если информация зашифрована с помощью K2, то расшифровать ее можно только с использованием ключа K1.
На практике один ключ называют секретным, а другой - открытым. Секретный ключ содержится в тайне владельцем пары ключей. Открытый ключ передается вместе с информацией в открытом виде. Еще одной особенностью шифрования с открытым ключом является то, что если у абонента имеется один из ключей пары, другой ключ вычислить невозможно. Именно поэтому открытый ключ передается в открытом виде.
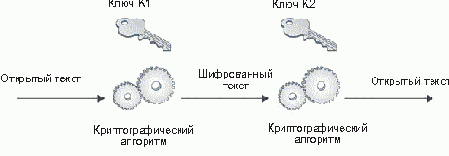
Рис. 12.8. Шифрование с открытым ключом
Если важно обеспечить конфиденциальность, шифрование выполняется с открытым ключом. Таким образом, расшифровать информацию может только владелец ключа, так как секретный ключ содержится в тайне самим владельцем. Если необходимо осуществлять аутентификацию, владелец ключевой пары шифрует данные с использованием секретного ключа. Корректно дешифровать информацию можно только с помощью правильного открытого ключа, передаваемого в открытом виде, и поэтому только владелец пары ключей (иными словами, хранитель секретного ключа) может отправлять информацию.
Целостность информации при передаче защищается в обоих случаях.
Целостность информации после передачи может быть проверена, если исходная информация была зашифрована с помощью секретного ключа владельца.
Недостатком систем шифрования с открытым ключом является то, что они требуют больших вычислительных мощностей и, следовательно, являются намного менее быстродействующими, нежели системы с секретным ключом. Тем не менее, если скомбинировать шифрование с открытым и секретным ключами, получится гораздо более мощная система шифрования. Система шифрования с открытым ключом используется для обмена ключами и аутентификации абонентов по обе стороны соединения. Система шифрования с секретным ключом затем используется для шифрования остального трафика.
Алгоритм обмена ключами Диффи-Хеллмана
Уитфилд Диффи (Whitfield Diffie) и Мартин Хеллман (Martin Hellman) разработали свою систему шифрования с открытым ключом в 1976 г. Система Диффи-Хеллмана (Diffie-Hellman) разрабатывалась для решения проблемы распространения ключей при использовании систем шифрования с секретными ключами. Идея заключалась в том, чтобы применять безопасный метод согласования секретного ключа без передачи ключа каким-либо другим способом. Следовательно, необходимо было найти безопасный способ получения секретного ключа с помощью того же метода связи, для которого разрабатывалась защита. Алгоритм Диффи-Хеллмана нельзя использовать для шифрования или дешифрования информации.
Алгоритм Диффи-Хеллмана работает следующим образом.
- Предположим, что двум абонентам (P1 и P2) требуется установить между собой безопасное соединение, для которого необходимо согласовать ключ шифрования.
- P1 и P2 принимают к использованию два больших целых числа a и b, причем 1 < a < b.
- P1 выбирает случайное число i и вычисляет I = ai mod b. P1 передает I абоненту P2.
- P2 выбирает случайное число j и вычисляет J = aj mod b. P2 передает J абоненту P1.
- P1 вычисляет k1 = Ji mod b.
- P2 вычисляет k2 = Ij mod b.
- Имеем k1 = k2 = ai*j mod b, следовательно, k1 и k2 являются секретными ключами, предназначенными для использования при передаче других данных.
Примечание
В приведенных выше уравнениях "mod" означает остаток. Например, 12 mod 10 = 2. Два - это остаток от деления 12 на 10.
Если злоумышленник прослушивает трафик, передаваемый по кабелю, то ему будут известны a, b, I и J. Тем не менее, остаются в секрете i и j. Уровень безопасности системы зависит от сложности нахождения i при известном I = ai mod b. Эта задача называется задачей дискретного логарифмирования и считается очень сложной (т. е. с помощью современного вычислительного оборудования ее решить практически невозможно), если числа очень велики. Следовательно, a и b необходимо выбирать очень тщательно. Например, оба числа b и (b - 1)/2 должны быть простыми и иметь длину не менее 512 бит. Рекомендуемая длина чисел составляет 1024 бит.
Алгоритм обмена ключами Диффи-Хеллмана используется во многих системах безопасности для реализации обмена ключами, используемыми для дополнительного трафика. Недостатком системы Диффи-Хеллмана является то, что она может быть уязвима для атаки посредником (см. рис. 12.9). Если атакующий сумеет разместить свой компьютер между двумя абонентами P1 и P2, подключить его к каналу связи и осуществлять перехват всей передаваемой информации, то он сможет выполнять обмен данными с P2, выдавая себя за P1, и с P1 под видом P2. Таким образом, обмен ключами будет происходить между P1 и злоумышленником и между P2 и злоумышленником. Тем не менее, осуществление такой атаки требует большого объема ресурсов, и в реальном мире такие атаки происходят редко.
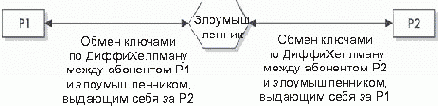
Рис. 12.9. Атака посредником на алгоритм Диффи-Хеллмана
Базовый алгоритм, позволяющий обеспечить конфиденциальность данных, очень прост.
Шифрованный текст = (открытый текст)e mod n Открытый текст = (шифрованный текст)d mod n Секретный ключ = {d, n} Открытый ключ = {e, n}
Безопасность обеспечивается сложностью вычисления d при наличии известных e и n. Подразумевается, что владелец пары ключей сохраняет секретный ключ в тайне, и что открытый ключ передается в открытом виде. Следовательно, если информация зашифрована с помощью открытого ключа, дешифровать ее может только владелец ключевой пары.
Также следует заметить, что алгоритм может быть обращен для обеспечения аутентификации отправителя. В этом случае алгоритм будет иметь следующий вид.
Шифрованный текст = (открытый текст)d mod n Открытый текст = (шифрованный текст)e mod n Секретный ключ = {d, n} Открытый ключ = {e, n}
В целях аутентификации владелец шифрует информацию с использованием секретного ключа. Это может делать только владелец ключевой пары, так как секретный ключ содержится в тайне. Любое лицо может дешифровать информацию и удостовериться в том, что данные поступили именно от владельца ключевой пары.
Генерация ключей RSA
При генерировании ключей RSA необходимо соблюдать тщательность. Чтобы сгенерировать ключевую пару RSA, выполните следующие шаги:
- Выберите два простых числа p и q и содержите их в секрете.
- Вычислите n = pq.
- Вычислите ф(n) = (p - 1)(q - 1).
- Выберите такое e, чтобы оно было взаимно простым по отношению к ф(n).
- Определите такое d, чтобы (d)(e) = 1 mod ф(n) и d < ф(n).
Примечание
Число n должно содержать порядка 200 знаков или больше. Тогда оба числа p и q должны иметь длину, по крайней мере, 100 знаков. Ключи для использования на практике должны иметь длину 1024 бит. В случае с секретной информацией рекомендуется использовать ключи длиной 2048 бит и более.
Реальный пример работы RSA
Имейте в виду, что мною выбраны числа, которые относительно легко проверить при выполнении данного примера. В реальном мире в алгоритме RSA используются гораздо большие числа.
- Сначала я выбрал два простых числа. В данном случае были выбраны числа p = 11 и q = 13.
- Теперь вычисляем n = pq. Имеем n = 11 * 13 = 143.
- Теперь нужно вычислить ф(n) = (p - 1)(q - 1) = (11 - 1)(13 - 1) = 10 * 12 = 120.
- Выбираем число e так, чтобы оно было простым относительно ф(n). Здесь было выбрано значение e = 7.
- Необходимо определить такое d, чтобы (d)(e) = 1 mod ф(n). Следовательно, (d)(7) = 1 mod 120; d должно также быть меньше 120. Находим, что d = 103. (103 умножаем на 7 и получается 721. 721 делим на 120 и получаем 6 с остатком 1.)
- Секретный ключ: {103, 143}.
- Открытый ключ: {7, 143}.
Для выполнения непосредственно шифрования и дешифрования используем исходные формулы.
Шифрованный текст = (открытый текст)e mod n Открытый текст = (шифрованный текст)d mod n
Предположим, что нужно отправить сообщение "9". С помощью формулы шифрования получаем следующее:
Шифрованный текст = (9)7 mod 143 = 48.
При получении зашифрованной информации она подвергается обработке алгоритмом дешифрования:
Открытый текст = (48)103 mod 143 = 9.
Другие алгоритмы с открытым ключом
Существуют некоторые алгоритмы с открытым ключом, имеющие такие же свойства, как RSA и алгоритм Диффи-Хеллмана. В данном параграфе мы вкратце рассмотрим три наиболее распространенных алгоритма.
Алгоритм Эль-Гамаля
Эль-Гамаль (Taher Elgamal) разработал вариант системы Диффи-Хеллмана. Он усовершенствовал алгоритм Диффи-Хеллмана и получил один алгоритм для шифрования и один для обеспечения аутентификации. Алгоритм Эль-Гамаля не был запатентован (в отличие от RSA) и, таким образом, стал более дешевой альтернативой, так как не требовалась уплата лицензионных взносов. Так как этот алгоритм базировался на системе Диффи-Хеллмана, безопасность информации при его использовании обеспечивается сложностью решения задачи дискретного логарифмирования.
Алгоритм цифровой подписи
Алгоритм Digital Signature Algorithm (DSA) был разработан правительством США как стандартный алгоритм для цифровых подписей (для получения дополнительной информации по цифровым подписям обратитесь к следующему параграфу).
Данный алгоритм базируется на системе Эль-Гамаля, но позволяет осуществлять только аутентификацию. Конфиденциальность этим алгоритмом не обеспечивается.
Шифрование с использованием эллиптических кривых
Эллиптические кривые были предложены для использования в системах шифрования в 1985 г. Системы шифрования с использованием эллиптических кривых (ECC) базируются на другой сложной математической задаче, нежели факторизация или дискретное логарифмирование. Данная задача заключается в следующем: имея две точки A и B на эллиптической кривой, такие что A = kB, очень трудно определить целое число k. Существует ряд преимуществ использования ECC перед алгоритмом RSA или Диффи-Хеллмана. Самым большим преимуществом является то, что ключи имеют меньшую длину (по причине сложности задачи), в результате чего вычисления производятся быстрее с сохранением уровня безопасности. Например, безопасность, обеспечиваемая 1024-битным ключом RSA может быть обеспечена 160-битным ключом ECC. Может пройти немало времени, прежде чем ECC будут полностью приняты к использованию, так как в этой области еще необходимо провести ряд исследований, и на существующие ECC зарегистрировано несколько патентов.
Вопросы для самопроверки
- Открытый текст преобразуется в ____________ в процессе шифрования.
- К какому типу систем шифрования относится DES?